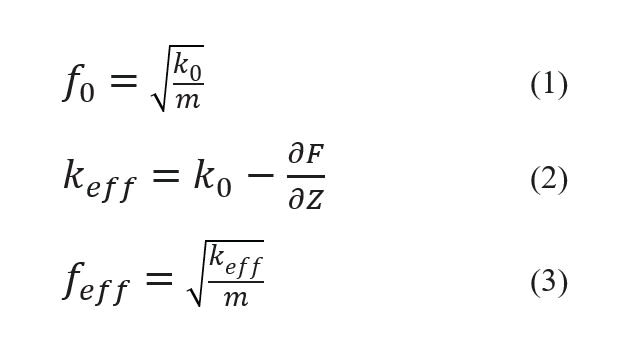Tapping mode is a dynamic AFM technique that images the sample topography by scanning the surface with an oscillating cantilever.
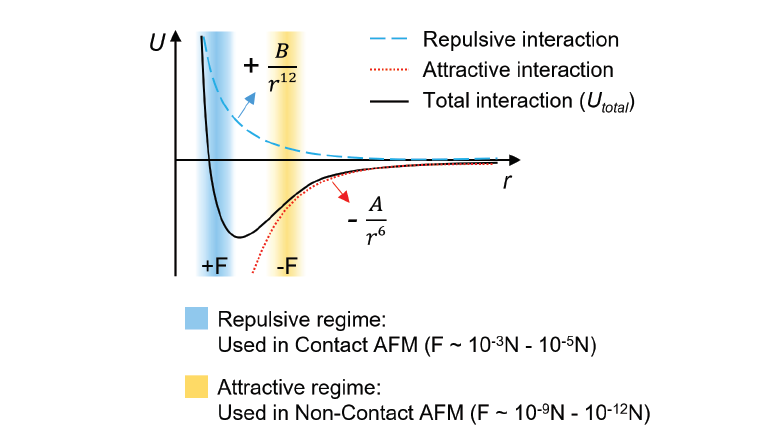
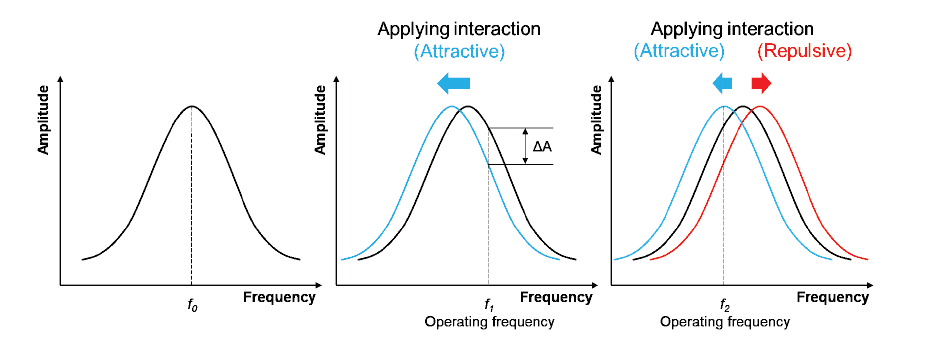
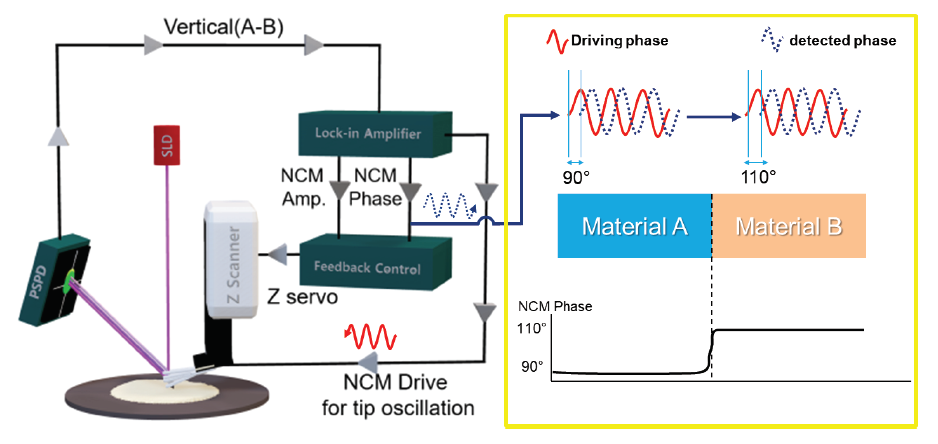
Similar to Park’s True Non-contact mode, Tapping mode uses the amplitude of cantilever oscillation to detect changes in the tip-sample interaction forces and thereby the sample topography. However, in Tapping mode the cantilever vibrates with larger amplitudes compared to True Non-contact mode and the tip makes intermittent contact with the sample surface during the measurement. The amplitude is used as topography feedback, while the phase lag be-tween drive and detected signal contains information about material-specific mechanical properties. Figure 1 shows the interatomic interaction potential, the so-called Lennard-Jones potential, which is used as approximation for the tip-sample interaction. At short distances between the atoms, the interaction is governed by short-ranged repulsive forces, mainly due to the Pauli repulsion, which prohibits the overlap of electron clouds of tip and sample. Above a certain threshold, attractive van der Waals forces dominate the interaction. Van der Waals forces originate from dipole-dipole interactions.