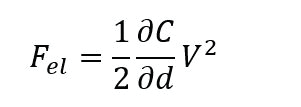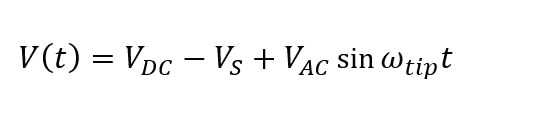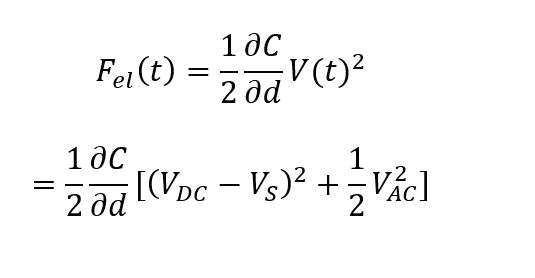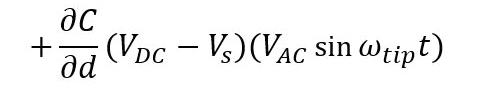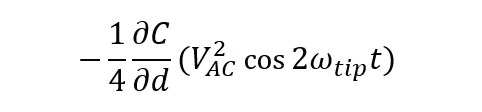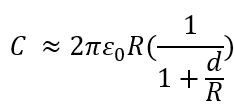High Resolution and High Sensitivity Imaging of Electrostatic Force
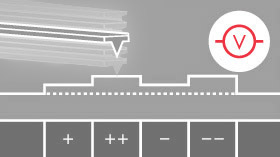
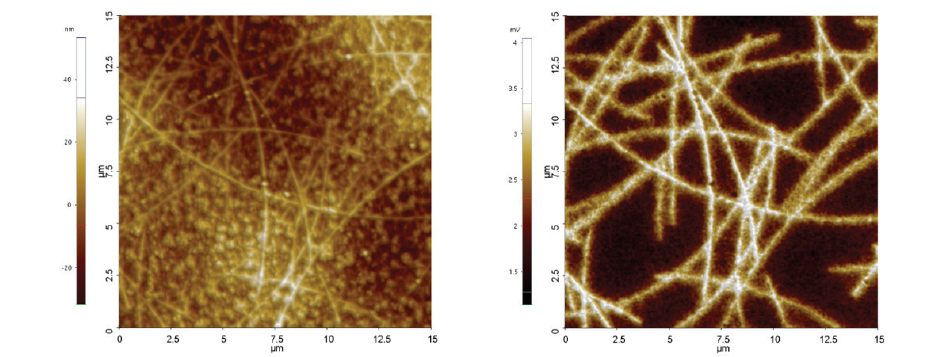
Electrostatic force microscopy (EFM) maps electrical properties of a sample surface by detecting the electrostatic force between the surface and a biased AFM tip. EFM applies a voltage between the tip and the sample while the cantilever oscillates above the surface, without contact. During the scan of the sample surface, the presence of electrostatic forces leads to a change in the oscillation amplitude and phase in the vertical deflection signal (figure 1). Therefore, the resulting EFM amplitude and phase images contain information about electrical properties such as the surface potential, charge distribution and dielectric constant on the sample surface.
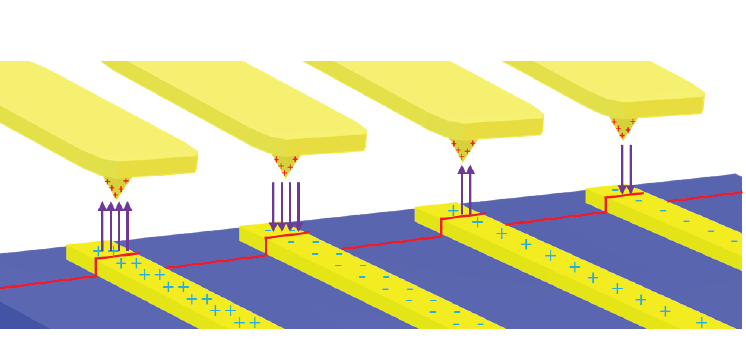
Figure 1. Electrostatic force acting between a metal coated tip and locally charged domains on the sample surface. The EFM amplitude and phase image the magnitude and sign of the charging, respectively.
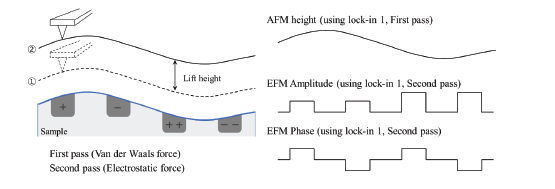
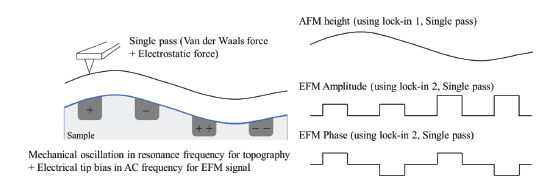
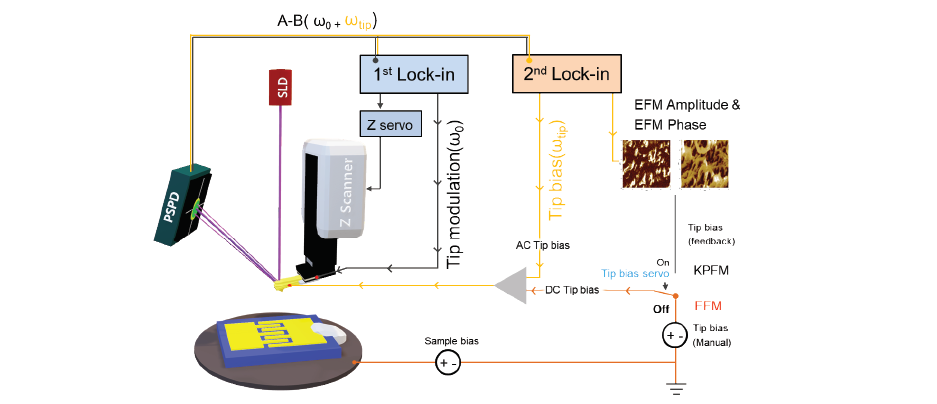
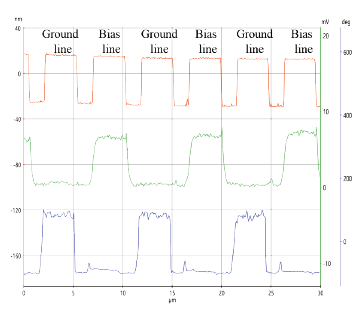
For EFM, the relevant interaction force to image the electrical properties of the sample surface is the electrostatic force between the biased tip and the sample. However, in addition to the electrostatic force, short-ranged van der Waals forces act between the tip and the sample surface. These van der Waals forces are used to measure the surface topography. There are two main approaches to decouple the electrostatic and van der Waals forces. The first approach exploits the different distance-dependence of the electrostatic and van der Waals forces by employing a dual pass lift-mode technique. The second single pass approach uses a different frequency for the detection of the electrostatic force than for topography imaging. Here, the van der Waals force and electrostatic force are decoupled by using an additional lock-in amplifier for the EFM signal. Figure 2 shows the two approaches for force decoupling. The obtained signals from both techniques contain information on the surface topography (called ‘Height’) and the electrical properties of the surface (called ‘EFM amplitude’ and ‘EFM phase’) generated by van der Waals and electrostatic forces, respectively. The two different measurement approaches are introduced separately in the following.