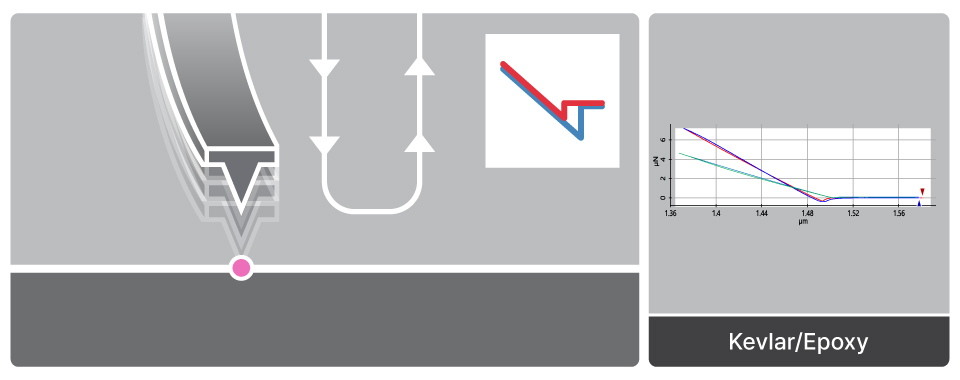
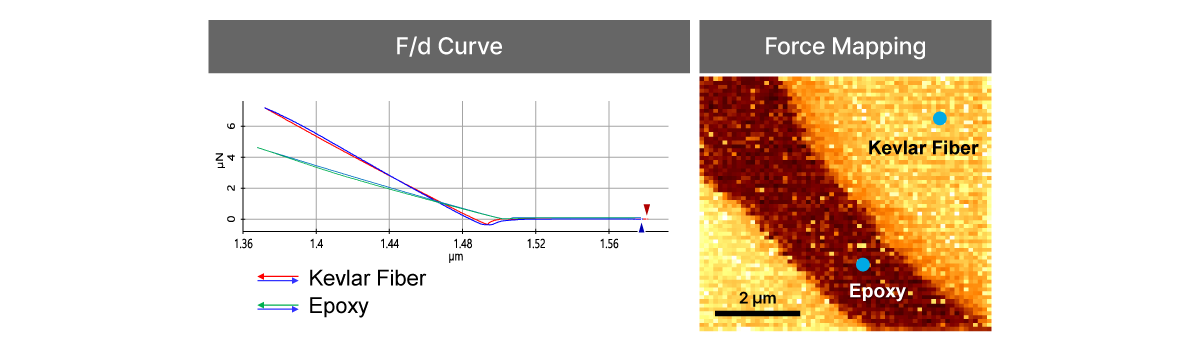
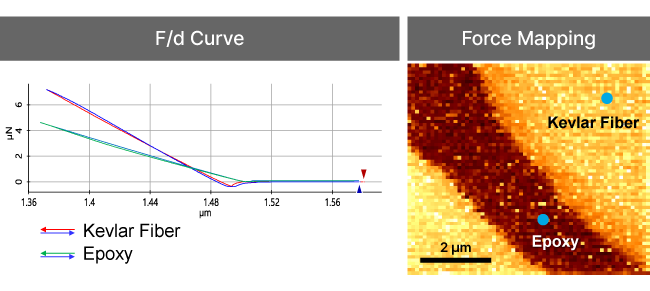
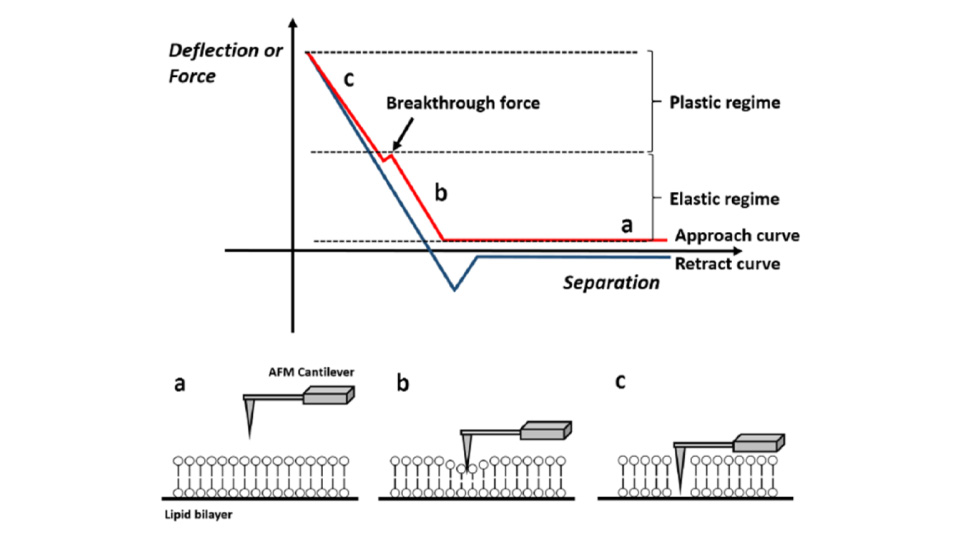
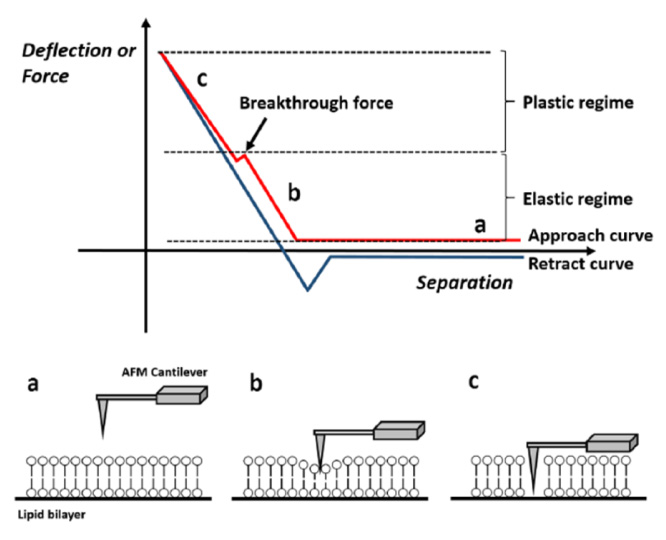
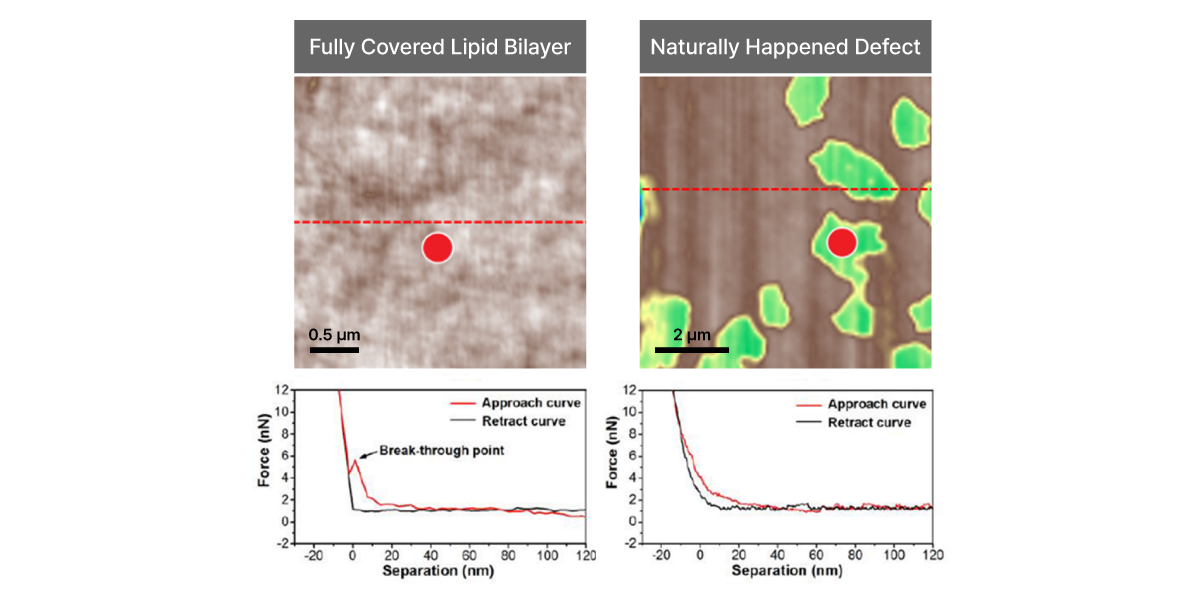
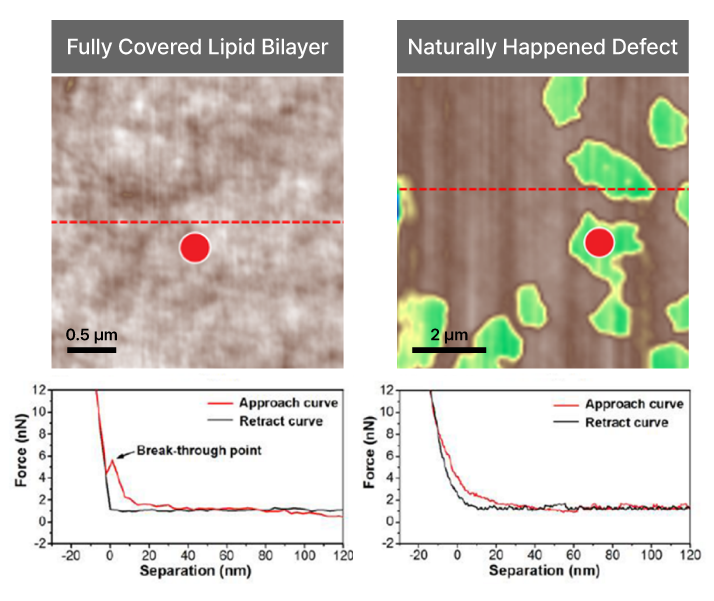
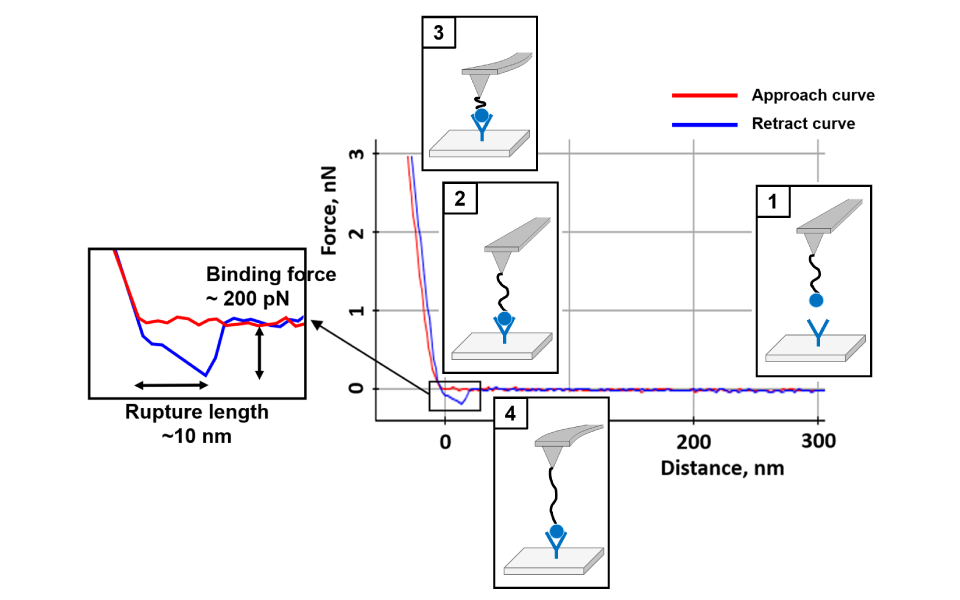
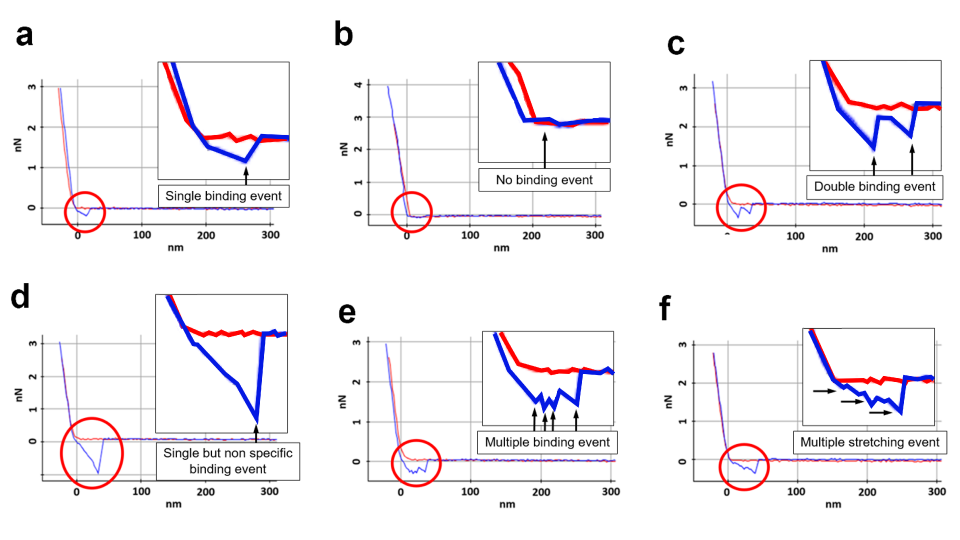
Force-distance Spectroscopy
F/d Spectroscopy
Mechanical property analysis by recording cantilever deflection relative to controlled tip–sample distance during approach and retraction cycles